The first continuous variable (CV) quantum key distribution (QKD) protocol using coherent states was limited to 3 dB of loss [1]. One way to overcome this limit was by applying post-selection on the data [2].

No switching protocol

The ANU quantum optics group has a long history in CV-QKD. In 2004, Christian Weedbrook proposed a no-switching protocol that uses a dual-homodyne measurement to simultaneously measure two conjugate quadratures [3,4]. Besides simplifying the existing protocol because we do away with switching between measurement bases, it also results in a higher key rate. This was demonstrated in an end-to-end experiment in 2005 by Andrew Lance and Vikram Sharma [5,6]. Previous demonstrations were proven secure against individual attacks and without excess noise. In 2007, Thomas Symul extended this to collective attacks and also in the presence of excess noise [7].

Discrete variable QKD excursions

In 2006, Syed Assad considered a variant of the BB84 protocol where the secret keys are generated via one-way communication instead of the usual two-way communication [8]. In this variant, Alice and Bob do not need to announce their basis choice. In fact, Bob does not need to communicate anything to Alice. This protocol turns out to be slightly less robust to errors than the original BB84. The security of QKD boils down to finding a bound on Eve’s information on the raw key. For individual attacks, this is a problem is one of finding the accessible information on a set of states. This problem is summarised by Jun Suzuki in this 2007 book chapter [9].

The secret keys in QKD are usually based on the measurement outcome. In 2014, Syed Assad proposed two protocols in which the secret keys are based on the measurement settings rather than the measurement outcomes [10]. In these protocols, Alice prepares an entangled state and send one half to Bob. Bob encodes his signal by the choosing how to measure this qudit which he then returns to Alice. This work was not related to the rest of CV-QKD projects but was a fun distraction.

Noiseless linear amplifiers to improve QKD rates

Back to CV-QKD. In 2013 Nathan Walk introduced a Gaussian post-selection protocol for CV quantum key distribution by linking the Gaussian post-selection to a noiseless linear amplifier (NLA) [11]. In 2014, Helen Chrzanowski used a measurement-based noiseless linear amplification (MB-NLA) to demonstrate entanglement distillation of the post-selected data [12]. It was shown that this can extend the secure communication distance for quantum key distribution.

One sided device independent QKD

In 2016, Nathan Walk and Sara Hosseni performed an experimental demonstration of one-sided device independent (1sDI) QKD with various different configurations [13]. A 1sDI-QKD is relevant in the setting where one party is in a secure central hub, such as a bank or government institution while other users are in less secure satellite stations which are inherently more vulnerable to hardware hacking attacks.

Parameter estimation for QKD using the method of moments

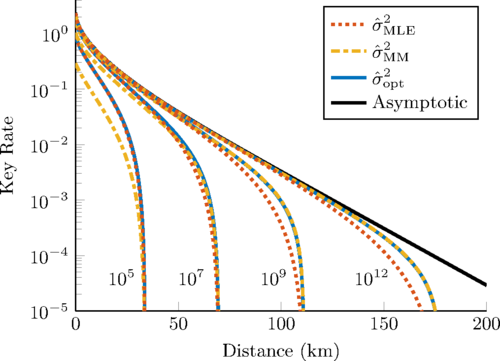
With finite sized data, estimation of channel parameters becomes important and good estimation techniques can extend the range and increase the key rate of CV-QKD protocols. In 2016, Oliver Thearle used the method of moments for channel parameter estimation which can lead an increase in the key rate by an order of magnitude [14].

QKD on a chip

In collaboration with Nanyang Technological University in Singapore, we demonstrated a proof-of-principle CV-QKD system on a silicon photonic chip [15]. All components except the laser source, including the modulators, multiplexers and homodyne detectors, are integrated on a silicon photonic chip. By integrating all the optical components on a silicon photonic chip, we have realized a stable, miniaturized and low-cost system for continuous-variable QKD (CV-QKD) that is compatible with the existing fibre optical communication infrastructure.

References

[1] F. Grosshans and P. Grangier, “Continuous variable quantum cryptography using coherent states,” Physical review letters, vol. 88, no. 5, p. 057902, 2002.

[2] C. Silberhorn, T. C. Ralph, N. Lütkenhaus, and G. Leuchs, “Continuous variable quantum cryptography: Beating the 3 dB loss limit,” Physical review letters, vol. 89, no. 16, p. 167901, 2002.

[3] C. Weedbrook, A. M. Lance, W. P. Bowen, T. Symul, T. C. Ralph, and P. K. Lam, “Quantum cryptography without switching,” Physical review letters, vol. 93, no. 17, p. 170504, 2004.

[4] C. Weedbrook, A. M. Lance, W. P. Bowen, T. Symul, T. C. Ralph, and P. K. Lam, “Coherent-state quantum key distribution without random basis switching,” Physical Review A, vol. 73, no. 2, p. 022316, 2006.

[5] A. M. Lance, T. Symul, V. Sharma, C. Weedbrook, T. C. Ralph, and P. K. Lam, “No-switching quantum key distribution using broadband modulated coherent light,” Physical review letters, vol. 95, no. 18, p. 180503, 2005.

[6] V. Sharma, A. M. Lance, T. Symul, C. Weedbrook, T. C. Ralph, and P. K. Lam, "A complete quantum cryptographic system using a continuous wave laser," In Photonics: Design, Technology, and Packaging II, vol. 6038, p. 603803. International Society for Optics and Photonics, 2006.

[7] T. Symul et al., “Experimental demonstration of post-selection-based continuous-variable quantum key distribution in the presence of gaussian noise,” Physical Review A, vol. 76, no. 3, p. 030303, 2007.

[8] S. M. Assad, J. Suzuki, and B.-G. Englert, “Raw-data attacks in quantum cryptography with partial tomography,” Int. J. Quantum Inf., vol. 4, no. 6, pp. 1003–1012, 2006.

[9] J. Suzuki, S. M. Assad, and B.-G. Englert, “Accessible information about quantum states: An open optimization problem,” Chapter, vol. 11, pp. 309–348, 2007.

[10] S. M. Assad and A. Kalev, “Encoding secret information in measurement settings,” International Journal of Quantum Information, vol. 12, no. 3, p. 1450016, 2014.

[11] N. Walk, T. C. Ralph, T. Symul, and P. K. Lam, “Security of continuous-variable quantum cryptography with Gaussian postselection,” Physical Review A, vol. 87, no. 2, p. 020303, Feb. 2013.

[12] H. M. Chrzanowski et al., “Measurement-based noiseless linear amplification for quantum communication,” Nature Photonics, vol. 8, no. 4, p. 333, 2014.

[13] N. Walk et al., “Experimental demonstration of gaussian protocols for one-sided device-independent quantum key distribution,” Optica, vol. 3, no. 6, pp. 634–642, 2016.

[14] O. Thearle, S. M. Assad, and T. Symul, “Estimation of output-channel noise for continuous-variable quantum key distribution,” Physical Review A, vol. 93, no. 4, p. 042343, 2016.

[15] G. Zhang, J. Y. Haw, H. Cai, F. Xu, S. M. Assad, J. F. Fitzsimons, X. Zhou et al., "An integrated silicon photonic chip platform for continuous-variable quantum key distribution," Nature Photonics, pp. 1–4, 2019.